kalkulator ATPOL
Można już łatwo określić współrzędne ATPOL'owe danego stanowiska używając mojego kalkulatorka ATPOL - wersja testowa, ale działająca jak dotąd poprawnie, sprawdzilem na kilku stanowiskach.
Jest jeszcze jeden drobny problem.
Może ktoś z szanownych kolegów i koleżanek przypadkiem zna, pamięta lub może odtworzyć ogólny wzór na określanie czy
punkt o współrzędnych (x0, y0)
znajduje się wewnątrz czy na zewnątrz
czworokąta o rogach (x1, y1), (x2, y2), (x3, y3) (x4, y4)
Kalkulatorek jest prawie idealny - z jednym mankamentem - kwadraty ATPOL'owe mają boki nieco nierównoległe do osi X i Y i mój algorytm określenia czasem nie trafia (wtedy nie poda wyniku).
Sprawdziłem.
Podałem współrzędne N 52 15' 58"
E 20 52' 24"
Jeśli dobrze pamiętam to chyba jest zasada, że jako pierwszą podaje się szerokość, a jako drugą długość.
No i mam wynik ADPOL ED-15
Zrobiłem symulację.
Kiedy wprowadzę dane z ED-15 to cel zostaje trafiony 3-4 km obok.
Zrobiłem kilkanaście transferów ze współrzędnych geograficznych na współrzędne ATPOL.
Przy podawaniu współrzędnych z dokładnością do sekundy kalkulator kilka razy nie trafił (nie podał współrzędnych)
Przy podawaniu danych z dokładnością do minuty, czy nawet dziesiętnej sekundy "trafienia" kalkulatora były stuprocentowe.
Boguś. Teraz współrzędne z tabeli ADPOLU wprowadź na mapę.
Zobacz co uzyskasz.?
Nie wiem czy do końca wiem o co chodzi:-)
Wg mnie współrzędne określają nazwijmy to "rogi" danego pola.
To pole z tego co pamiętam ma 10x10 km, więc nasze stanowisko określane wg ATPOL leży "gdzieś" w tym polu.
Dopiero posłużenie się dokładnymi współrzednymi - takimi co do sekundy (jeśli takie dane mamy możliwość uzyskać) pozwala nam dosyć precyzyjne dotrzeć do miejsca znaleziska, posługując się odpowiednio szczegółową mapą.
Tak mi się przynajmniej wydaje???
Kolejność została zmieniona na szerokość/długość. Dzięki za zwrócenie uwagi.
Nie za bardzo rozumiem testu - współrzędne z tabeli ADPOLU wprowadź na mapę. Które współrzędne i na jaką mapę?
I co względem czego jest przesunięte? To ważne.
Drugie. To co Bogdanowi nie wychodziło. Ponieważ kwadraty ADPOL są "skoszone" względem siatki geograficznej, w obecnej wersji wyszukiwania właściwego kwadratu nie podaję współrzędnych ADPOL - jeśli punkt znaduje się "w cieniu" tego skosu; bo nie chcę podać mylnie kwadratu.
Stąd moje pytanie o algorytm - może ktoś ma bliżej do szkoły :) i pamięta. Wiem że coś takiego się liczyło ale to było 20 lat temu :)
Jakby nikt nie miał pod ręką to poszperam po podręcznikach: (
Jeszce jedno - dokładność podania wsp. geograficznych nie ma znaczenia przy znajdowaniu kwadratu we współrzędnych ADPOL.
Jak podasz
N53st E18st to poszuka punktu N53st00'00" E18st00'00"
Jak podasz
N53st15' E18st35'
to poszuka w jakim kwadracie jest punkt
N53st15'00" E18st53'00"
Oczywisice 53 - 18 i 53 15' 18 35' to punkty leżace gdzie indziej, choć być może akurat w tym samym kwadracie.
Tu mogę potwierdzić, że "chybione" strzały kalkulatorka miały miesce w okolicach "styku" poszczególnych pól, czyli prawdopodobnie trfiały w rzeczony "cień".
Wystarczało jednak zaokrąglić którą kolwiek ze współrzędnych do dziesietnej sekundy i było po problemie:-)
Przypuszczam, że w przypadku trafienia w okolice "styku" rogów czterech pól będzie należało to zaokrąglenie zwiększyć przy dwóch współrzednych - nie mam pojęcia jak duży "cień" może powstać w takich ekstremalnie niekorzystnych punktach?
Ten "cień" to tylko przejściowo - aż poprawię algorytm. Dlatego jest to wersja testowa kalkulatora.
Wtedy pozostanie tylko jeden problem - co robić z punktem leżącym dokładnie na styku kwadratów - do którego kwadratu zaliczyć - nie znalazłem (Ania też szukała) informacji jak są domknięte kwadraty. Chyba przyjmę arbitralnie, że są domknięte od góry i z lewej. To drobiazg ale czystość metody cierpi :)
U nas się pisze od góry i z lewej więc na "chłopski rozum"...:-)
Czystość (jakby co) musi się więc ugiąć:-)
Symulacje przeprowadziłem tutaj:
To moje namiary:
N 52 15 58
E 20 52 24
Kalkulator wskazuje ED-15
Z tabeli ADPOLU odszukuję namiar na ED-15 i mam:
N 52 15 13
E 20 54 15
Wprowadzam te dane na mapę.
No i jestem w punkcie oddalonym od mojego o ok. 3-4 km; biorąc pod uwagę skalę mapy.
Wykonajcie podobną symulację dla obranego przez Was punktu.
Sprawdzimy w jakim przedziale rozrzutu się znajdziecie.
Nie wiem jakie to może mieć znaczenie dla naszego
przedsięwziecia, bo rozrzut jest dość znaczny.
Wynika ze wskazań ADPOLU, że moje "rzadkości" nie rosły wcale w lesie, tylko w obszarze zabudowanym.
np. w miejscu, gdzie jest budynek.
Marku,
To co bierzesz z siatki ADPOL
N 52 15 13
E 20 54 15
to jest namiar na dolny-prawy róg pola o symbolu ED15.
Wszystkie cztery "namiary" wokół cyfry 15 to kolejne "rogi" pola ED15
Teraz już rozumiem. Chyba nie tak zrozumiałeś co to jest "współrzędna ADPOL" - to numer kwadratu o powierzchni 100km2.
Innymi słowy Twoje namiary
N 52 15 58
E 20 52 24
są gdzieś w kwadracie ED-15 ale nie w jego południowo-wschodnim rogu
N 52 15 13
E 20 54 15
a gdzies w srodku, w punkcie:
N 52 15 58
E 20 52 24
Współrzędne rogów kwadratu odczytujesz z tabeli ADPOL i są one równe:
róg pół-zach róg pół-wsch
20°45’41” 20°54’29”
52°20’44” 52°20’36”
ED-15
20°45’28” 20°54’15”
52°15’21” 52°15’13”
róg poł-zach róg poł-wsch
Jest to obszar o powierzchni 100km2. Tak, że na podstawie takiej informacji plus nazwa dzielnicy Warszawy nikt się konkretnego miejsca ze smardzówką - bez dodatkowych informacji od Ciebie, nie doszuka.
Dzięki, dzięki. Zasada kwadratu ADPOLU już jasna. Mój pewien nawek zupełnie z innej beczki zamieszał mi w głowie. Cel to cel.
Najważniesze, że działa. Zsada pojęta. Etap został zrealizowany.
100km2 przeczesać za grzybkiem, nawet fajna zagadka.
Uff. Musiałem sobie przypomnieć geometrię linni na płaszczyźnie w układzie współrzędnych.
Kalkulator działa już bez "cienia" i powinien znajdować odpowiedź dla wszystkich punktów na terenie Polski.
No chyba, że coś jeszcze nie działa :)
Wygląda na to, że działa :)
A tak z czystej ciekawości to jak jest w końcu z tym punktem o współrzędnych (x0, y0)?
Znajduje się wewnątrz czy na zewnątrz?
Odpowiedź na to pytanie też mnie ciekawi bo zdaje się figura o współrzędnych (x1, y1), (x2, y2), (x3, y3) (x4, y4) nie jest czworokątem tylko odcinkiem:-)
A kalkulator działa bez zarzutu. Sprawdzałem na kilku lokalizacjach, których numery kwadratów ATPOL znałem.
Darku, chyba chodzi o figurę zbudowaną na tych punktach, czyli odcinkach
(x1, y1), (x2, y2)
(x2, y2), (x3, y3)
(x3, y3), (x4, y4) oraz
(x1, y1), (x4, y4)
bo Marek pisał o czworokącie o takich ROGACH a nie odcinkach.
ps. nie będzie to 4-kąt, jeśli conajmniej 3 X-y lub Y-ki będą sobie równe, prawda?
(wiadomość edytowana przez pimpek 05. Lutego. 2005)
Więc doszukałem się tylko takiego równania prostej.
y-y1 = a * (x-x1)
z tego wyprowadziłem sobie co trzeba i zastosowałem.
Ostatnia wersja kalkulatora oprócz tego, że działa chyba o. k. to pokazuje jeszcze obrazek. Uznałem to za przydatne, raz w ocenie poprawności obliczeń, dwa widać czy punkt jest w pobliżu granicy kwadratu - jeśli tak to można się postarać o dokładne współrzędne geograficzne bo może stanowisko jest po drugiej stronie granicy kwadratu - jeśli dokładnie zmierzyć jego współrzędne.
Wszelkie poprzednio chybione strzały, które kalkulatorek teraz są idealne.
Dodanie graficznej prrezentacji umiejscowienia punktu w kwadracie ze wszech miar wskazane.
Czy załączona www.mapapolski.pl[mapapolski.pl] w skali 1: 70 000 jest najdokładniejszą z możliwych do uzyskania drogą internetową?
W posiadanych przeze mnie (różnych wydawców z lat 60 i 70) mapach w skali 1: 25 000 brak siatki współrzednych geograficznych lub są inne.
Czy ktoś wie jak jest na mapach bardziej aktualnych naszym czasom?
Sprawę załatwia GPS ale to jednak znaczny wydatek:- (
Opcja w www.mapapolski.pl[mapapolski.pl] Zaznacz na mapie punkt o współrzędnych mogłaby być bardzo przydatna gdyby ktoś kogoś prosił o uzupełnienie danych ze stanowiska, pobrania eksykatu itp. bo był w odległym terenie przejazdem, na wczasach itd.
Czy ktoś słyszał o systemie map topograficznych V MAP2, czy te mapy są dostępne przeciętnemu obywatelowi?
W inernecie podobnie jak lista Wildsteina jest dostępny zeskanowany komplet wojskowych map Polski 1: 50000 z lat 70/80. Ich zaleta to stosunkowo duza dokladnosc (sa zaznaczone oddziały leśne i drogi oddziałowe) no i rogi mapy mają konkretne współrzędne geograficzne (w układzie (datum) Pulkovo 1942 (1) wg. OziExplorera). Najlepiej ogląda się te mapki pod OziExplorerem gdzie po skalibrowaniu współrzędnymi z rogów można pod kursorkiem spokojnie odczytać współrzędną dowolnego punktu z mapy.
Co do nakierowania chętnego, to najskuteczniejszy jest dobry "opis jak trafić" plus ewentualnie jako dodatkowy środek wsp. geograficzne.
A czy ze wspomnianych przez Marka wojskowych mapek da się bezpośrednio (tzn. bez użycia jakiegoś programu) odczytać współrzędne geograficzne?
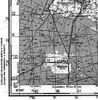
Wkleiłem fragment takiej mapki:
bio-forum.pl" alt="mapka">
i jak widać jest na niej siatka i z każdej strony dwa rzędy liczb (wewnątrz i na zewnątrz ramki) - jak odszyfrować z tego współrzędne?
MOże teraz wejdzie:
bio-forum.pl" alt="mapka">
Tak, to te mapki o których pisałem wyżej.
Ekierka.
Na marginesie sa kropki - w pionie jest ich 60 na 10minut tj. każda kropka to 10 sekund. Prościej chyba ściągnąć OziExplorer lub coś analogicznego.
Nie jeste pewien ale może być problem w systemach (datum) na tych mapach jest układ Pulkowo 1942. W GPS i na niektórych nowych mapach turystycznych domyślnie jest WGS 84.
Punkt o takiej samej długości i szerokości geograficznej w jednym i drugim systemie różni się w terenie w zależności od rejonu Polski do kilkuset metrów.
Np. punkt wg. Pulkovo 1942 - 51s30' 17s15'
to WGS 84 - 51s28'59, 5" 17s14'53. 1"
Program do oglądania map typu OziExplorer dba o to aby automatczynie konwertować to w dowolną stronę. No i masz współrzędne pod kursorem (nie potrzeba ekierki).
Współrzędne geograficzne na tych mapkach są tylko w rogach mapy - arkusze maja 15min długości i 10 minut szerokości geograficznej - wartości pomiędzy rogami mapy trzeba interpolować jak wyżej opisałem.
Ciekawy artykuł
Szybko i wygodnie:-)
Bogdanie ale niezbyt dokładnie.
Przy dużych połaciach leśnych czy też innych jednolitych terenach, z małą liczbą punktów charakterystycznych, w przypadku określenia ATPOL-u dla punktu leżącego na granicy kwadratów mogą wystąpić problemy.
Ale faktycznie bardzo szybkie i wygodne w innych miejscach.
Dla punków spornych lepsza jest jednak mapa Google Earth z nakładką. Ustawiasz widok z satelity i masz każde drzewo czy też krzak widoczny.
Gdyby ktoś to przerobił na nakładkę na Google Earth wtedy nie tylko szybka i wygodna ale wręcz fantastyczna bo byłaby bardzo dokładna.
Ale jakby głębiej zastanowić się, to czy nam aż tak dokładne narzędzie potrzebne?
Faktycznie dokładne określenie miejsca jest kłopotliwe, ale ma jedną fajną sprawę, naniesione granice powiatów i gmin. Ja używam tej strony do określenia gminy.
Dla zainteresowanych:
www.botany.pl/atpol[botany.pl]
Nowa strona o ATPOL z matematycznym modelem i dostępnymi narzędziami do obliczeń. Także z siatką 1x1 km.
Myślę że jest to zdecydowanie wygodniejsze (i precyzyjniejsze) od kalkulatora mojego autorstwa.
Stosowną rekomendację, przekierowującą, umieściłem:
Trzymamy się tematu forum. Nie drażnimy się. Ma być miło :) ⇒ szerzej o zasadach i coś jak regulamin